Doğrular ve Açılar

DOĞRULAR VE AÇILAR

Atatürk’ün Geometri Kitabı

Atatürk, ölümünden bir buçuk yıl kadar önce üçüncü Türk Dil Kurultayı' ndan hemen sonra 1936 - 1937 yılı kış aylarında kendi eliyle “Geometri” isimli bir kitap yazmıştır. Bu 44 sayfalık yapıttaki boyut, uzay, yüzey, düzey, çap, yarıçap, kesit, çember, teğet, açı, açıortay, iç ters açı, dış ters açı, taban, eğik, kırık, yatay, düşey, yöndeş, konum, üçgen, dörtgen, beşgen, köşegen, eşkenar, ikizkenar, paralelkenar, yanal, yamuk, artı, eksi, çarpı, bölü, toplam, oran, orantı, türev, alan, varsayım, gerekçe gibi terimler Atatürk tarafından türetilmiştir. Bu konu ile ilgili Ömer L. Örnekol’un anısı aşağıda verilmiştir.

Atatürk, lise müdürü matematik öğretmeni Ömer Beygo ve müdür başyardımcısı felsefe öğretmeni Faik Dranaz ve öteki ilgililerle birlikte, doğrudan doğruya liseye geldiler. Burada

ilkin, 4 Eylül 1919’ da tarihî kongrenin toplandığı kongre salonunu ve özel odaları gezdiler ve duygulandılar. Sonra topluluk hâlinde lisenin 9/A sınıfının geometri (o zamanki adıyla hendese) dersine girdiler. Bu derste bir kız öğrenciyi tahtaya kaldırdılar. Öğrenci, tahtada çizdiği koşut iki çizginin başka iki koşut çizgiyle kesiştiğini, kesişmesinden oluşan açıların adlarını söylemekte zorluk çekiyor ve yanlışlıklar yapıyordu. Bu durumdan etkilenen Atatürk, tepkisini “Bu anlaşılmaz terimlerle öğrencilere bilgi verilemez. Dersler, Türkçe yeni terimlerle anlatılmalıdır.” diyerek belirtti ve tebeşiri eline alıp tahtada çizimlerle “zaviye”nin

karşılığı olarak “açı”, “dılı”nın karşılığı olarak “kenar”, “müsellesin” karşılığı olarak “üçgen” gibi Türkçe yeni terimleri kullanarak birtakım geometri konularını ve bu arada Pisagor teoremini anlattılar.

Kazanımlar Neler?

M.7.3.1.1. Bir açıyı iki eş açıya ayırarak açıortayı belirler.

Dinamik geometri yazılımlarından yararlanılabilir.

M.7.3.1.2. İki paralel doğruyla bir kesenin oluşturduğu yöndeş, ters, iç ters, dış ters açıları belirleyerek özelliklerini inceler; oluşan açıların eş veya bütünler olanlarını belirler; ilgili problemleri çözer.

a) Aynı düzlemde olan üç doğrunun birbirine göre durumları ele alınır.

b) İki doğrunun birbirine paralel olup olmadığına karar vermeye yönelik çalışmalara da yer verilir. Bunu yaparken doğruların ortak kesenle yaptığı açıların eş olma durumlarından yararlanılır.

Neler Öğreneceğiz?

§        Doğru ve açı nedir?

§        Açıortay nedir ve nasıl oluşturulur?

§        İki paralel doğru ile bir kesenin oluşturduğu açılar nelerdir?

§        Bu açıların özellikleri nelerdir?

§        Eş veya bütünler açı nasıl belirlenir?

HATIRLATMA!

Doğru: Her iki yönden de sonsuza kadar giden aynı doğrultudaki noktalar kümesidir. Tek boyutludur ve sadece uzunluğu vardır fakat uzunluğu ölçülemez. Sınıfta tahtaya veya defterlerimize çizdiğimiz doğrular aslında gerçek doğru değildir.Gerçek doğru çizilemez. Çünkü sonsuza kadar devam ettiremeyiz. Biz sadece doğru modeli çizebiliriz. Bir ip hayal edin ve bu ipin sonsuzdan gelen ve sonsuza giden uçları olduğunu düşünün ya da bir lastiğin uçlarının sonsuza kadar çekildiğini hayal edin.

Doğruyu isimlendirirken genelde ya küçük harf kullanırız ya da doğrunun üzerinde bulunan iki noktayı kullanırız:

•      d  doğrusu
•      AB doğrusu gibi

(Doğru modeli)    

Işın: Bir noktadan başlayıp sonsuza giden aynı doğrultudaki noktalar kümesidir. Işının uzunluğu ölçülemez ve gerçek ışın çizilemez. Biz sadece ışının modelini çizebiliriz. Günlük yaşamımızda karşımıza çıkan ışın modellerine çivi, kurşun kalem,şerit metre, örgü şişi gibi nesneleri örnek verebiliriz.

Işın isimlendirilirken başlama noktası ile üzerindeki bir nota kullanılır. OA ışını denir.

Açı: Başlangıç noktaları aynı olan iki ışının arasındaki açıklığa açı denir. Açı ölçülebilirdir. Açıyı belirtmek için açıyı oluşturan noktaların üstüne "^" sembolü koyulur. Açı ölçüsü ise " m(...)" şeklinde ifade edilir. Açıyı ölçmek için açı ölçer kullanırız. Açı ölçüsünün birimi "derece"dir. Günlük hayatımızda ev çatısı, duvar kesişimleri, kavşaklar, vücut-kol arası, saat gibi birçok örnek verilebilir.

    

         

Buraya kadarki kısım  5. ve 6. sınıfta öğrendiğimiz bazı kavramları hatırlamamız için hazırlanmıştır.

AÇIORTAY  Nedir?

Başlangıç noktası açının köşesi olup, açıyı iki eşit açıya bölen ışın veya doğru parçasına denir.                                          

     

• Açıortay ile birbirinden ayrılmış eşit açılar şekil üzerinde aynı sembol veya işaret ile gösterilir.

MÖ 4. yüzyıl – Geometrik araçlar

Yunan filozof Platon, gerçek bir geometricinin aletlerinin düz bir kenar ve bir pergel ile sınırlı olması gerektiğini ve bunun böylece geometrinin pratik bir ustalıktan ziyade bir bilim olarak kurulmasına yardım edeceğini belirtmiştir.

Şimdi bizde pergelimizi elimize alalım!!!!!!

Bir Açının Açıortayı Nasıl Çizilebilir?

Malzemeler: Kalem, cetvel, pergel ve açı ölçer.

ADIMLAR:

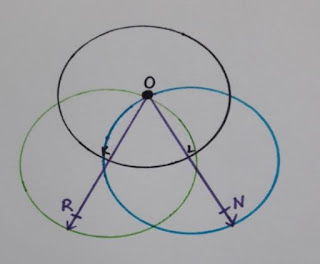
1)Cetvelimizi kullanarak [OR ve [ON ışınlarını çizelim.

3) Pergelimizin sivri ucunu O noktası üzerinde sabitleyelim ve merkezi O olacak ve [OR, [ON ışınlarını kesecek biçimde bir çember çizelim. Kestiği noktalar da K ve L  noktaları olsun.

4) Şimdi pergelimizin açıklığını bozmadan ilk önce sivri ucu K noktasına koyalım ve merkezi K noktası olan bir çember çizelim. İkinci olarak pergelimizin açıklığını bozmadan sivri ucu  L noktasına koyalım ve merkezi L noktası olan bir çember daha çizelim. Çemberlerin dışarıda  kesiştiği nokta da M noktası olsun.

Öneri: Telefonumuza veya bilgisayarımıza yükleyebileceğimiz bir program olan  GeoGebra, bizlere açıortay da dahil olmak üzere birçok kavramı elde edebilmemizde yardımcı olacaktır. Aşağıda linkini bıraktığım adreslerde bunun örneklerini rahatlıkla görebilirsiniz.

• https://www.youtube.com/watch?v=jRzKOPckjn8

• https://www.youtube.com/watch?v=_c1pN8RaMG8

• https://www.youtube.com/watch?v=cr4BvdfKuvQ

    Geogebra’da açıortay çizimiJ

Uygulanabildiği durumda, elimizde pergelimiz cetvelimiz yoksa, açıortayının bulunması istenen bir açının kollarını üst üste getirdiğimizde oluşan hat aslında o açının açıortayı olur. Bunun için yağlı kağıt kullanabiliriz. J

Acaba başka bir açıortay çizim metodu bulabilir misiniz?

Soru Çözerken Önemli Noktalar!

NOT: Bir şekilde açıortay olarak verilen ışının sağ ve solundaki açılar eşittir.

BU KONUDA ÖĞRENECEKLERİMİZ:

• Aynı düzlemdeki üç doğrunun birbirine göre durumu
•  Üç doğrunun birbirine göre durumlarına örnekler
• Paralel, kesen, ortak dikme, noktadaş doğrular

ÜÇ DOĞRUNUN BİRBİRİNE GÖRE DURUMLARI

Aynı düzlem olan üç doğru birbirine göre şu durumlarda aşağıda verilmiştir:
1) Üç doğru birbirine paralel olur.
2) Üç doğru bir noktada kesişir. Aynı noktadan geçen bu üç doğruya “Noktadaş Doğrular” denir.
3) Doğrular ikişer ikişer birbirini keser. Bu durumda üçgen oluşur.
4) İki doğru birbirine paralel olur ve üçüncü doğru bunları keser. Paralel doğruları bir noktada kesen bu doğruya “Kesen” adı verilir.
5) İki doğru birbirine paralel olur ve üçüncü doğru bunları dik keser. Buradaki kesen doğru diğer iki doğrunun dikmesi olduğu için bu doğruya “Ortak Dikme” adı verilir.
6) Üç doğru çakışık olabilir.
7) Doğrulardan ikisi çakışırken diğeri bunları kesebilir.


Şimdi ise bu tanımların şekillerine bakalım:

BU KONUDA ÖĞRENECEKLERİMİZ:

•  İç Açılar, Dış Açılar, Ters Açılar
•  Yöndeş Açılar, İç Ters Açılar, Dış Ters Açılar
•  Bütünler Açılar, Eş Açılar

PARALEL İKİ DOĞRUYLA BİR KESENİN OLUŞTURDUĞU AÇILAR

 İç Açılar

İç Ters Açılar

Dış Açılar

Dış Ters Açılar

Eş Açılar

KARŞI DURUMLU AÇILAR

Paralel iki doğru arasında kalan ve birbirine bakan açılara karşı durumlu açılar denir. Karşı durumlu açılar bütünlerdir.

Bütünler açılar;
a ile b b ile c
c ile d a ile d
e ile f e ile h
h ile g f ile g’dir.

Paralel iki doğruyu üçüncü bir doğrunun kesmesiyle oluşan açılardan aynı yöne bakan açılara yöndeş açılar denir.

Düzlemde farklı iki paralel doğruyu iki farklı noktada kesen doğru, bu doğruların kesenidir.
Paralel iki doğru bir kesenle kesildiğinde sekiz tane açı meydana gelir.

m ve n paralel doğrularının k doğrusu ile A ve B noktalarında kesişerek oluşturdukları açılar durumlarına göre adlandırılırlar.


 Bunları Unutmayalım!!!!!

İki Doğrunun Paralel Olmasını Anlama:

·         İki doğru birbirine paralel ise ortak hiçbir noktaları mevcut değildir.

·         İki doğru birbirine paralel ise asla kesişmezler.

Şimdi de yeni nesil bir soru baksak fena olmaz!!!

        Etkinlik Yapmaya Ne Dersiniz!!!

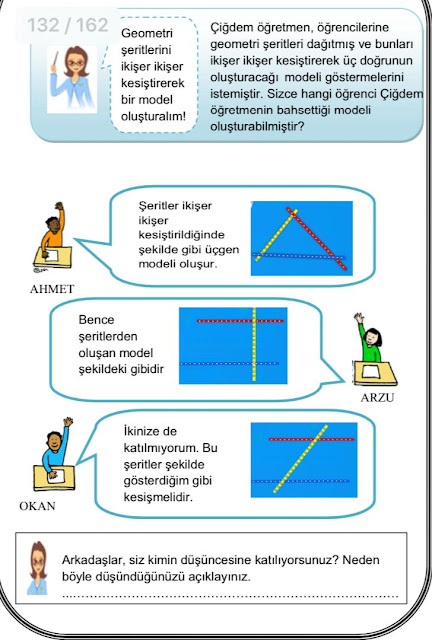
Bu geometri şeritlerimizle 3 doğrunun birbirine göre durumlarını rahatlıkla inceleyebiliriz. Böylece konuyu daha iyi pekiştirmiş oluruz.

KONUMUZ GÜNLÜK YAŞAMDA NERELERDE VAR?

Resimleri inceleyelim.

Masanın kenarını ve ayaklarını birer doğru modeli olarak düşünürsek bu doğruların birbirlerine göre konumu nasıldır?

Koşu yolu üzerindeki beyaz çizgileri birer

doğru modeli olarak düşünürsek bu doğruların birbirlerine konumu nasıldır?

Uçurtmanın çıtalarını birer doğru modeli olarak 

düşünürsek bu doğruların birbirlerine göre konumu nasıldır?

   Aşağıda verdiğimiz örneklerde de doğru parçalarını yine bir doğru modeli olarak hayal edersek daha kolay anlamış oluruz.

                                         

Balkonumuzda      Kapılarımızda

Konumuzun çözümlü örneklerine bakalım:

 

OYUN ZAMANI

Isınma

1. Öğrenciler iki blok halinde yan yana dizilir.

2. Her öğrenci kendisini düzlemde bir nokta olarak hayal eder.

3. Müzik başladığında öğrenciler yan yana yürümeye başlarlar.

4. Müzik durduğunda her öğrenci kollarını açarak doğru olur. Öğrenciler oluşan doğruların birbirlerine göre durumlarını açıklar.

5. Müzik tekrar başladığında bu sefer öğrenciler karışık olarak yürümeye başlarlar. Müzik durduğunda ise tekrar hepsi doğru olur ve oluşan doğruların birbirine göre durumları açıklanır. Paralel, çakışan ve dik doğrular varsa belirlenir. Oluşan açıların ne tür açılar oldukları söylenir.

Oyun

1. Sınıf 4 gruba ayrılır.

2. Her gruba sırayla konuya ilişkin bir kavram verilir. Bu kavramlar: ışın, paralel doğrular, çakışan doğrular, orta dikme, yöndeş açılar, iç ters açılar, dış ters açılar ve doğru demetidir

3. Gruplar sırayla bu kavramları bir dakika içinde sessiz film oynayarak diğer gruplara anlat-maya çalışır.

4. Kavram bulunursa, kavramı bulan grup 10 ve kavramı anlatan grup 5 puan alır ve oyun sı-rayla devam eder.

Canlandırma

Birbirleriyle daha önce hiç karşılaşmamış olan üç insanın hayatları bir gün kesişir. Bu üç insanın da hayatları birer doğru olarak düşünüldüğünde bu kesişmeler nasıl ve kaç farklı durumda olabilir?

1. Bu durumlardan birisini seçilerek bir hikâye oluşturulur.

 2. Bu hikâyede bu üç insana karakter, yaş ve meslek gibi özellikler verilir.

3. Hikâyenin canlandırması yapılır.

4. Canlandırma sonunda üç insanın hayat çizgileri doğrular şeklinde tahtaya çizilerek birbirlerine göre konumları açıklanır.

KAYNAKÇA

Van de Walle, J. A., Karp, K. S., Bay- Williams, J. M. (2013). İlkokul ve Ortaokul Matematiği: Gelişimsel Yaklaşımla Öğretim, ( çeviri). Ankara: Nobel Yayıncılık

Dane, A. ve Başkurt, H. (2011). İlköğretim 6, 7 ve 8. Sınıf Öğrencilerinin Doğru Parçası, Doğrusallık, Işın ve Açı Kavramlarını Algılama Düzeyleri, Erzincan Eğitim Fakültesi Dergisi, 13(2):85-103

https://www.bilgicik.com/yazi/7-sinif-dogrular-ve-acilar-konu-anlatim/

https://www.dersimis.com/dogrular-ve-acilar/dogrular-ve-acilar-konu-anlatimi/1144-7-sinif-dogruda-acilar-konu-anlatimi.html

https://www.matematikciler.com/7-sinif-paralel-iki-dogrunun-bir-kesenle-yaptigi-acilar/

https://www.matematikciler.com/7-sinif-uc-dogrunun-birbirine-gore-durumu/

https://www.egitimhane.com/7-sinif-dogruda-acilar-d57095.html

7.sınıf matematik ders kitabı

http://www.atam.gov.tr/dergi/sayi-63/ataturkun-hazirladigi-geometri-terimleri-kitabi

Göksu, F.C.( 2014).Doğrular, Açılar ve Çokgenler Konularının Kavram Karikatür Destekli Yapılandırmacı Öğrenme Yaklaşımına Göre İşlenmesi,(Yüksek Lisans Tezi),PAÜ,Eğitim Bilimleri Enstitüsü, Denizli.

Yenilmez, K. Ve Uygan, C. (2010). Yaratıcı Drama Yönteminin İlköğretim 7.Sınıf Öğrencilerinin Geometriye Yönelik Öz- Yeterlilik İnançlarına Etkisi, Kastamonu Eğitim Dergisi,18,(3): 931-942.

Rabia KÖSE 1711210036

Yağmur KUMBUL 1711210023

İlköğretim Matematik Öğretmenliği 3/B